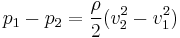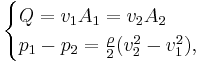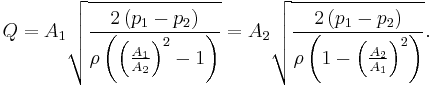Venturi effect

The Venturi effect is the reduction in fluid pressure that results when a fluid flows through a constricted section of pipe. The Venturi effect is named after Giovanni Battista Venturi (1746–1822), an Italian physicist.

Contents

Background

The Venturi effect is a jet effect; as with a funnel the velocity of the fluid increases as the cross sectional area decreases, with the static pressure correspondingly decreasing. According to the laws governing fluid dynamics, a fluid's velocity must increase as it passes through a constriction to satisfy the principle of continuity, while its pressure must decrease to satisfy the principle of conservation of mechanical energy. Thus any gain in kinetic energy a fluid may accrue due to its increased velocity through a constriction is negated by a drop in pressure. An equation for the drop in pressure due to the Venturi effect may be derived from a combination of Bernoulli's principle and the continuity equation.

The limiting case of the Venturi effect is when a fluid reaches the state of choked flow, where the fluid velocity approaches the local speed of sound. In choked flow the mass flow rate will not increase with a further decrease in the downstream pressure environment.

However, mass flow rate for a compressible fluid can increase with increased upstream pressure, which will increase the density of the fluid through the constriction (though the velocity will remain constant). This is the principle of operation of a de Laval nozzle. Increasing source temperature will also increase the local sonic velocity, thus allowing for increased mass flow rate.

Referring to the diagram to the right, using Bernoulli's equation in the special case of incompressible flows (such as the flow of water or other liquid, or low speed flow of gas), the theoretical pressure drop at the constriction is given by:

p_1 - p_2 = \frac{\rho}{2}(v_2^2 - v_1^2)

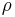where \rho\, is the density of the fluid, 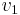v_1 is the (slower) fluid velocity where the pipe is wider, 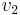v_2 is the (faster) fluid velocity where the pipe is narrower (as seen in the figure). This assumes the flowing fluid (or other substance) is not significantly compressible - even though pressure varies, the density is assumed to remain approximately constant.

Experimental apparatus

Venturi tubes

The simplest apparatus, as shown in the photograph and diagram, is a tubular setup known as a Venturi tube or simply a venturi. Fluid flows through a length of pipe of varying diameter. To avoid undue drag, a Venturi tube typically has an entry cone of 30 degrees and an exit cone of 5 degrees. To account for the assumption of an inviscid fluid a coefficient of discharge is often introduced, which generally has a value of 0.98.

Orifice plate

Venturi tubes are more expensive to construct than a simple orifice plate which uses the same principle as a tubular scheme, but the orifice plate causes significantly more permanent energy loss.[1]

Instrumentation and measurement

Venturis are used in industrial and in scientific laboratories for measuring the flow of liquids.

Flow rate

A venturi can be used to measure the volumetric flow rate Q .

Since

\begin{cases} Q = v_1A_1 = v_2A_2\\ p_1 - p_2 = \frac{\rho}{2}(v_2^2 - v_1^2) \text{,} \end{cases}

then

Q = A_1\sqrt{\frac{2\left(p_1 - p_2\right)}{\rho\left(\left(\frac{A_1}{A_2}\right)^2-1\right)}} = A_2\sqrt{\frac{2\left(p_1 - p_2\right)}{\rho\left(1-\left(\frac{A_2}{A_1}\right)^2\right)}} \text{.}

A venturi can also be used to mix a liquid with a gas. If a pump forces the liquid through a tube connected to a system consisting of a venturi to increase the liquid speed (the diameter decreases), a short piece of tube with a small hole in it, and last a venturi that decreases speed (so the pipe gets wider again), the gas will be sucked in through the small hole because of changes in pressure. At the end of the system, a mixture of liquid and gas will appear. See aspirator and pressure head for discussion of this type of siphon.

Differential Pressure

Main article: Pressure head

As fluid flows through a venturi, the expansion and compression of the fluids cause the pressure inside the venturi to change. This principle can be used in metrology for gauges calibrated for differential pressures. This type of pressure measurement may be more convenient, for example, to measure fuel or combustion pressures in jet or rocket engines.

Examples

The Venturi effect may be observed or used in the following:

A simple way to demonstrate the Venturi effect is to squeeze and release a flexible hose in which fluid is flowing: the partial vacuum produced in the constriction is sufficient to keep the hose collapsed.

Venturi tubes are also used to measure the speed of a fluid, by measuring pressure changes at different segments of the device. Placing a liquid in a U-shaped tube and connecting the ends of the tubes to both ends of a Venturi is all that is needed. When the fluid flows though the Venturi the pressure in the two ends of the tube will differ, forcing the liquid to the "low pressure" side. The amount of that move can be calibrated to the speed of the fluid flow.[1]

See also

External links

References

  1. ^ a b "The Venturi effect". Wolfram Demonstrations Project. http://demonstrations.wolfram.com/TheVenturiEffect/. Retrieved 2009-11-03.